The maximum fiber stress in bending for laterally supported beams and girders is Fb = 0.66Fy if they are compact, except for hybrid girders and members with yield points exceeding 65 ksi (448.1 MPa). Fb = 0.60Fy for non-compact sections. Fy is the minimum specified yield strength of the steel, ksi (MPa). Table lists values of Fb for two grades of steel.
The allowable extreme-fiber stress of 0.60Fy applies to laterally supported, unsymmetrical members, except channels, and to non-compact box sections. Compression on outer surfaces of channels bent about their major axis should not exceed 0.60Fy
The allowable stress of 0.66Fy for compact members should be reduced to 0.60Fy when the compression flange is unsupported for a length, in (mm), exceeding the smaller of
lmax=76.0bf/(Fy)½
lmax=20,000/Fyd/Af
where bf=width of compression flange, in (mm)
d=beam depth, in (mm)
Af =area of compression flange, in2(mm)2
The allowable stress should be reduced even more when l/rT exceeds certain limits, where l is the unbraced length, in (mm), of the compression flange, and rT is the radius of gyration, in (mm), of a portion of the beam consisting of the compression flange and one-third of the part of the web in compression.
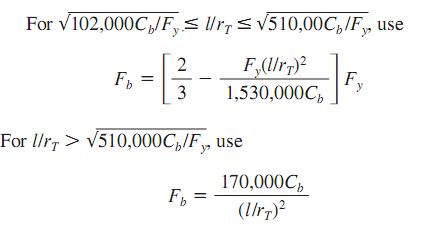
Where Cb =modifier for moment gradient
When, however, the compression flange is solid and nearly rectangular in cross section, and its area is not less than that of the tension flange, the allowable stress may be taken as
Fb=12,000Cb/ld/Af
When Eq. applies (except for channels), Fb should be taken as the larger of the values computed from Eqs above, but not more than 0.60Fy .
The moment-gradient factor Cb in Eqs. above may be computed from
Cb=1.75 + 1.05 M1/M2+ 0.3(M1/M2)2 less than equal to 2.3
Where M1 = smaller beam end moment, and M2 = larger beam end moment.
The algebraic sign of M1/M2 is positive for double curvature bending and negative for single-curvature bending. When the bending moment at any point within an unbraced length is larger than that at both ends, the value of Cb should be taken as unity. For braced frames, Cb should be taken as unity for computation of Fbx and Fby .
Equations can be simplified by introducing a new term:
Q=(l/rT)2Fy
Now, for 0.2 less than equal to Q ess than equal to 1,
Fb=(2 – Q)Fy/3
For Q > 1:
Fb=Fy/ 3Q
| Yield strength,ksi (MPa) | Compact0.66Fy (MPa) | Non-compact,0.60 Fy (MPa) |
| 36 ( 248.2) | 24 (165.5) | 22 (151.7) |
| 50 (344.7) | 33 (227.5) | 30 (206.8) |
The allowable extreme-fiber stress of 0.60Fy applies to laterally supported, unsymmetrical members, except channels, and to non-compact box sections. Compression on outer surfaces of channels bent about their major axis should not exceed 0.60Fy
The allowable stress of 0.66Fy for compact members should be reduced to 0.60Fy when the compression flange is unsupported for a length, in (mm), exceeding the smaller of
lmax=76.0bf/(Fy)½
lmax=20,000/Fyd/Af
where bf=width of compression flange, in (mm)
d=beam depth, in (mm)
Af =area of compression flange, in2(mm)2
The allowable stress should be reduced even more when l/rT exceeds certain limits, where l is the unbraced length, in (mm), of the compression flange, and rT is the radius of gyration, in (mm), of a portion of the beam consisting of the compression flange and one-third of the part of the web in compression.
Where Cb =modifier for moment gradient
When, however, the compression flange is solid and nearly rectangular in cross section, and its area is not less than that of the tension flange, the allowable stress may be taken as
Fb=12,000Cb/ld/Af
When Eq. applies (except for channels), Fb should be taken as the larger of the values computed from Eqs above, but not more than 0.60Fy .
The moment-gradient factor Cb in Eqs. above may be computed from
Cb=1.75 + 1.05 M1/M2+ 0.3(M1/M2)2 less than equal to 2.3
Where M1 = smaller beam end moment, and M2 = larger beam end moment.
The algebraic sign of M1/M2 is positive for double curvature bending and negative for single-curvature bending. When the bending moment at any point within an unbraced length is larger than that at both ends, the value of Cb should be taken as unity. For braced frames, Cb should be taken as unity for computation of Fbx and Fby .
Equations can be simplified by introducing a new term:
Q=(l/rT)2Fy
Now, for 0.2 less than equal to Q ess than equal to 1,
Fb=(2 – Q)Fy/3
For Q > 1:
Fb=Fy/ 3Q
0 Komentar Blog: